はじめに
この記事では、筑波大学と弊社の共同研究の成果である Graph Neural PDE Solvers with Conservation and Similarity-Equivariance について解説します。この研究により、非常に高い汎用性と信頼性を持ち、複雑な流体現象を予測可能な機械学習技術の基盤である FluxGNN と呼ばれる手法が完成しました。これにより、下図で示すような、軽い流体 (煙など) が上昇していくような現象に対しても高精度に予測することができるようになりました。以下では、本研究の目的・手法・結果について説明していきます。
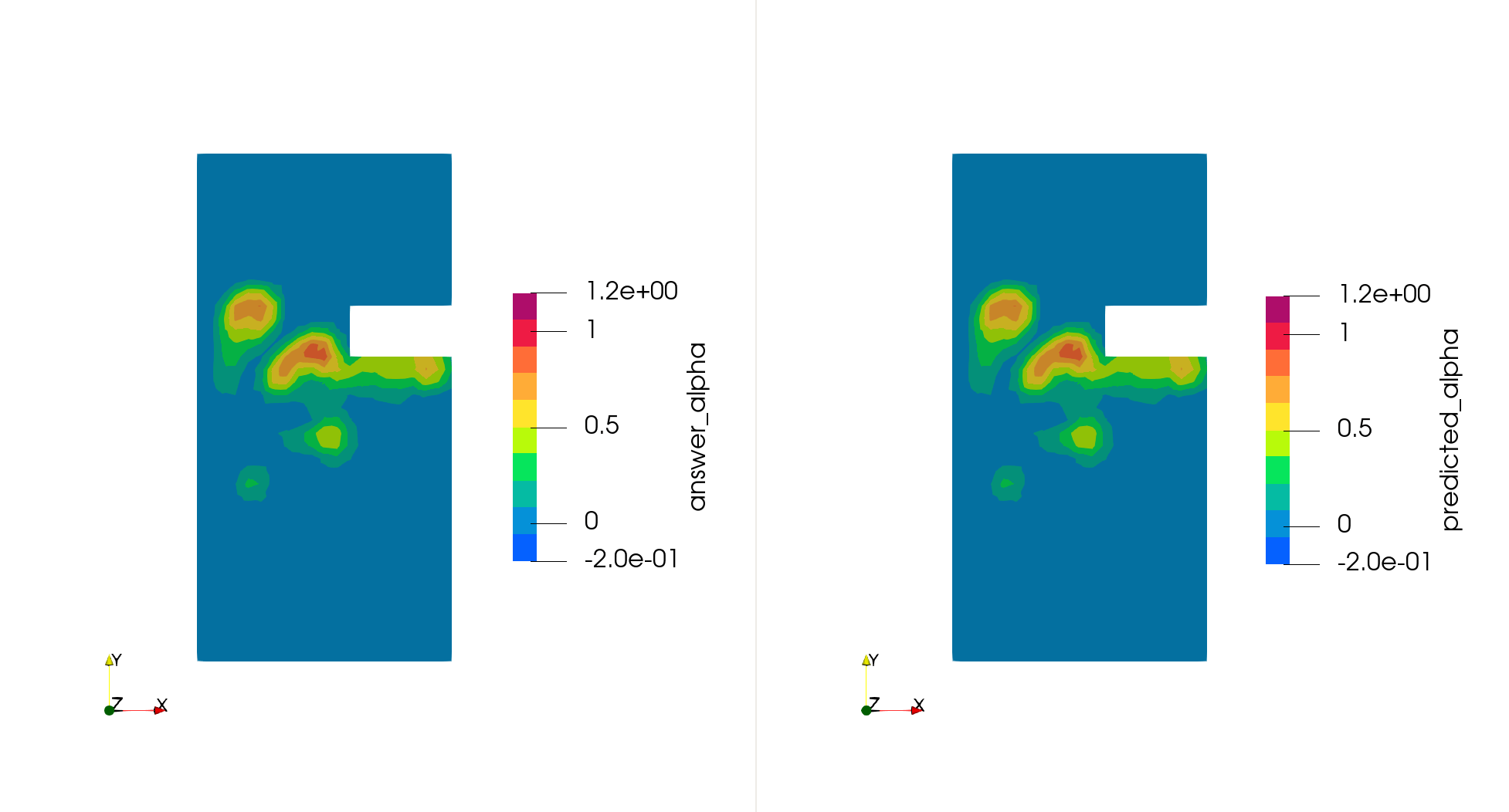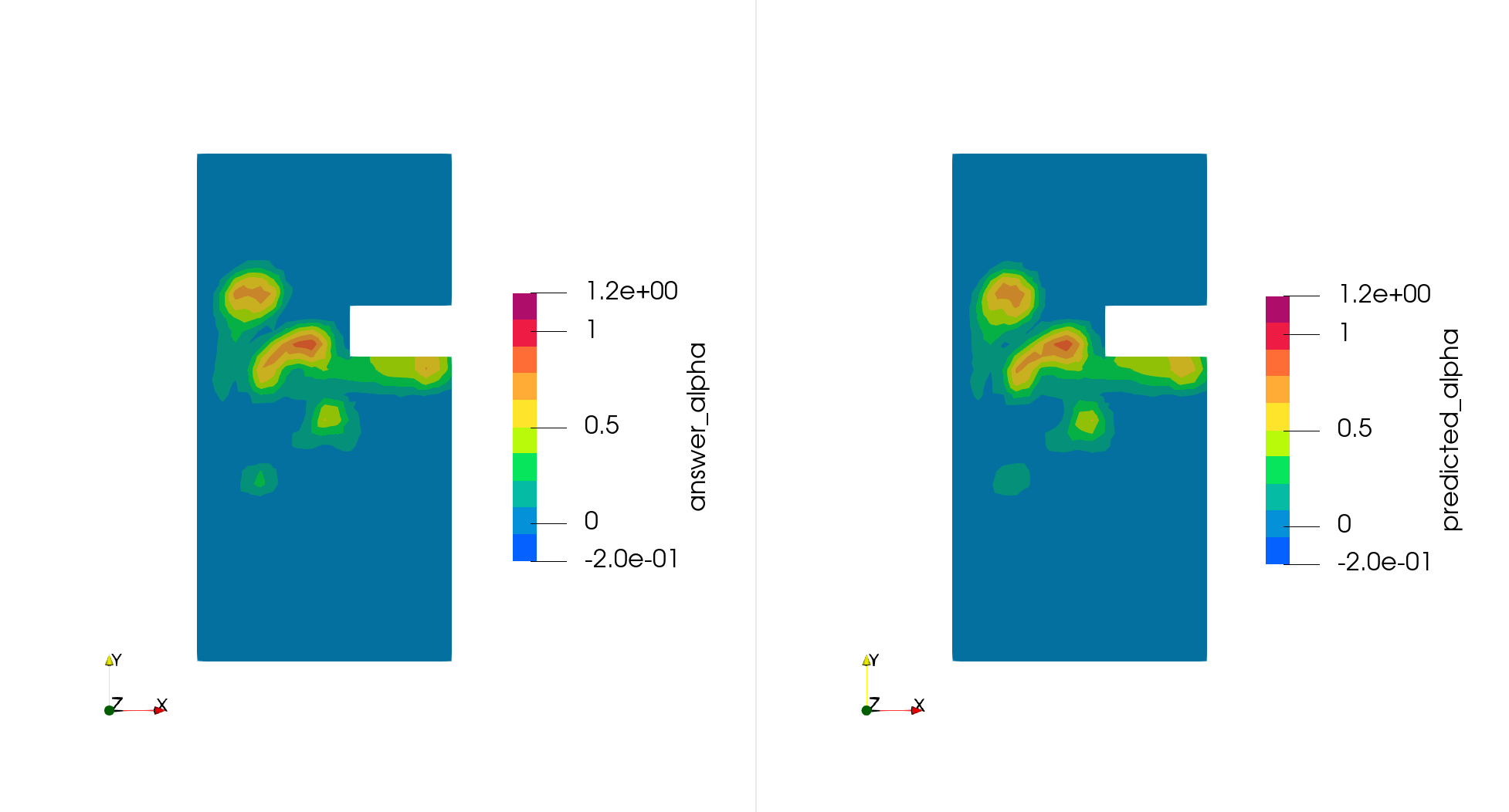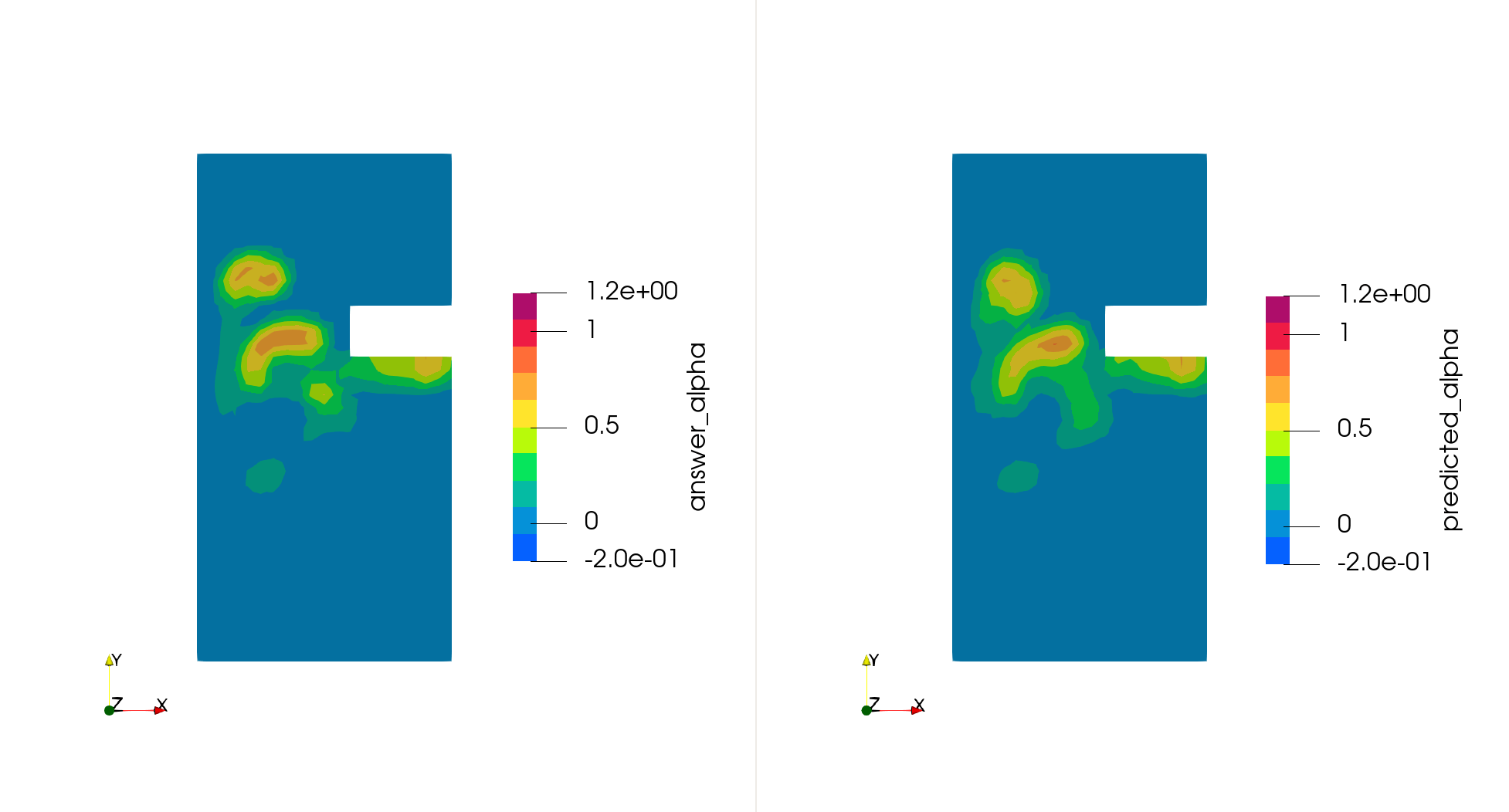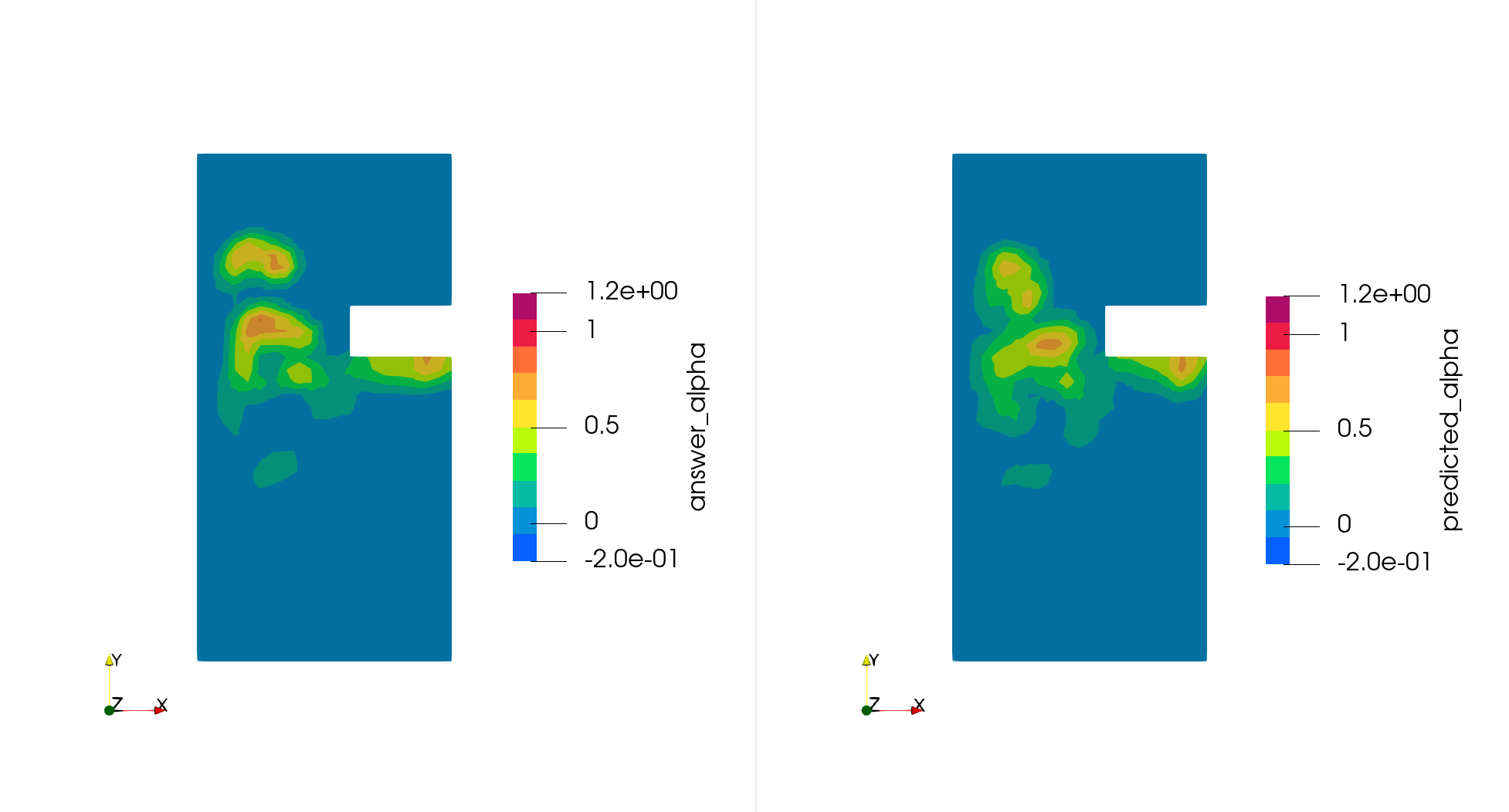
モチベーション
技術の詳細に入る前に、本研究のモチベーションを説明します。物理現象の予測に機械学習を用いるメリットの一般論として、下記のような可能性が考えられます:
- 計算の速さ: 過去のデータの情報を活用して予測を行うため、ゼロベースで計算を行う従来の物理シミュレーションよりも高速に予測を行える
- データへの適応性: データをもとに学習を行うため、従来の物理シミュレーションでは実験との乖離が大きくなるような対象に対しても高精度に予測を行える
- 最適化計算への適用可能性: 深層学習のモデルでは入力が微小に変化した際の出力の変化、すなわち感度が容易に計算できるため、感度を用いた最適化計算や逆問題への適用が容易に行える
そのため、機械学習を用いて物理シミュレーションの代替をする、サロゲートモデルの研究が盛んに行われています。しかしながら、機械学習ベースの予測モデルでは、学習したデータに近い条件であれば高精度に予測できたとしても、そうでない条件の場合に精度が大幅に劣化してしまうという汎化性能の欠如といった問題があります。特に、ものづくりの現場で用いられているような物理シミュレーションにこのような技術を適用する場合、多様な製品形状に対して評価を実施しなければならないため、形状に対する汎化性能は重要になります。
研究の指針
そこで本研究では、機械学習による予測モデルに汎化性能を付与するために、物理現象の持つ性質を機械学習モデルに組み込むことを考えました。具体的には、下記のふたつの性質です:
- 保存性: 全体の質量やエネルギーなどが時間変化に対して一定となる性質
- 対称性: 同じ現象に対して別の視点で観測しても現象の本質が変わらないという性質
このうち、対称性 (より正確には、相似変換についての対称性) についてもう少し詳しく説明します。例えば、同じ現象でも、視点を変えて (例えば首を傾けるなどして) 観測すると、対象は回転したように見えます。また、同じ現象でもそれを記述する単位系を変える (例えば、流速について m/s を使うか mm/h を使うかなど) ことによって物理量を表す数値は異なったものになります。したがって、下図のように、実際には同じ現象であっても、対応する物理量の数字の表現がまったく異なってしまうといったことが起こります。
これは通常の機械学習モデルにとっては都合がよくありません。なぜなら、通常の機械学習プロセスでは入力の数値と出力の数値の関係を学習によって獲得するわけですが、同じ意味のデータでもまったく異なる数値となる可能性があるためです。さらに、例えば長さを m の単位系で表したデータで学習したあとに mm の単位系のものを入力してしまうと数値は 1000 倍されてしまいますが、学習データに含まれていないような大きな数値が入力されてしまうため、大幅な外挿が起こり精度が低下していまいます。
単位の問題だけであればユーザが事前に単位系を揃えておけば問題ないのですが、流体現象では流れの複雑さを特徴づける Reynolds 数が同じであれば同様の現象が起きるという Reynolds の相似則が知られており、これは単位の変換だけでなくさまざまな大きさのスケール変換に対して成り立つものです。そのため、この性質を活かしたほうが少ない学習データでも学習を効率よく進めることができ、予測の信頼性も向上すると期待することは自然しょう。したがって、本研究ではこの保存性と対称性を機械学習モデルに組み込むことを目的としています。
FluxGNN のアイディア
では、どのように保存性と対称性を満たす機械学習モデルを作ればいいか、そのアイディアについて説明していきましょう。この節が、本記事でのもっとの重要なパートとなります。
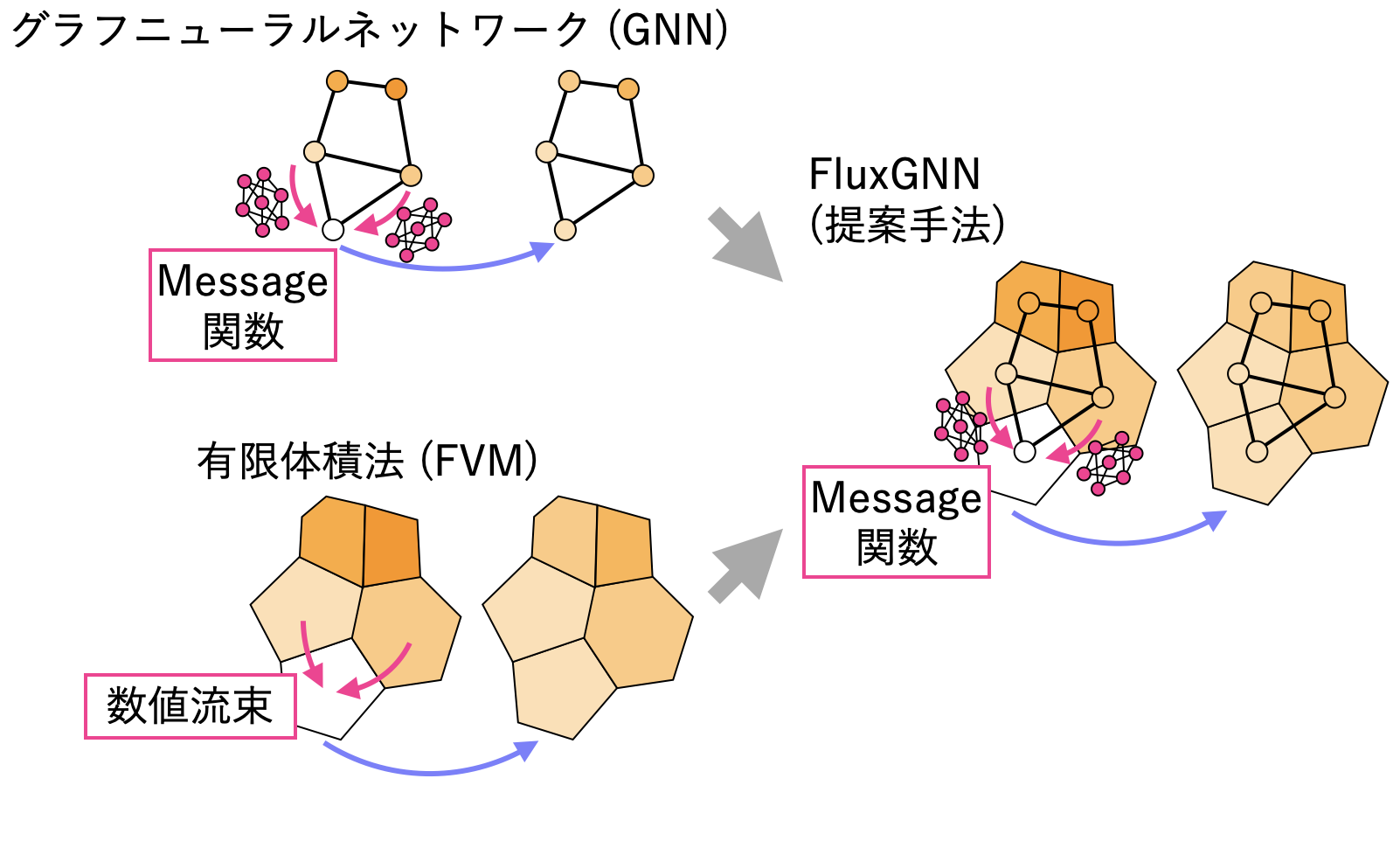
保存性を対称性を満たす機械学習モデルを構築するためには、既存の物理シミュレーションの手法が大いに参考になります。なぜなら、既存の物理シミュレーション手法ではそれらの物理現象の性質を満たすように構成されていることが多く、その定式化を紐解いていけば物理現象の性質を満たすための条件が得られると期待できるからです。本研究では特に、保存性 (より正確には空間局所的な保存性) と対称性を満たす、有限体積法 (FVM) を参考にすることで、保存性と対象性を満たす機械学習モデルである FluxGNN を構築しています。
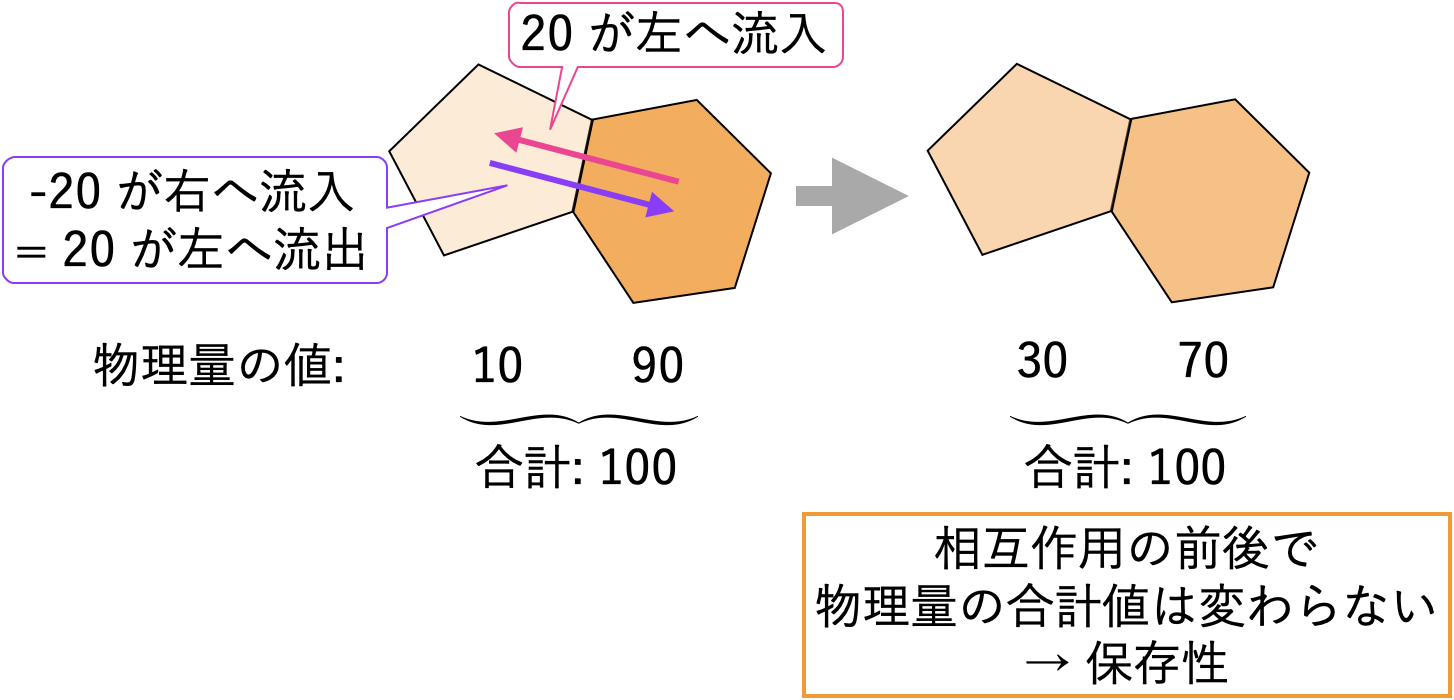
ここで、FVM がどのようにして保存性を担保しているかを簡単に見ていきましょう。上図のように、シミュレーションに用いるメッシュの隣り合っているふたつのセルの、何かしらの物理量 (流速や密度など) のやりとりに着目します。このとき、FVM では
(*) [右のセルから左のセルへの物理量の流入] = − [左のセルから右のセルへの物理量の流入]となるように物理量のやりとりを定式化します。これによりふたつのセル間の物理量のやりとりではその合計値が変わらないため、保存性が成り立つことがわかります1。この、セル間の物理量のやりとりを表す量は、セルという仮想的な概念上で数値的に決定されるものであることから、数値流束 (numerical flux) と呼ばれます。この数値流束の定式化のしかたにはさまざまな方法があり、それらによって物理シミュレーションの精度や安定性が変化します。したがって、物理シミュレーションの対象や目的に応じて適切な数値流束の定式化を選択する必要があり、その点が流体の物理シミュレーションを困難にしている要因のひとつになっています。
さて、上記の FVM の考え方をそのまま機械学習モデルに変換することを考えましょう。上記 (*) の関係が成り立ってさえいれば保存性が成立するため、数値流束の計算方法には任意性があるのでした。すなわち、 (*) の関係を成り立たせながら数値流束の計算をニューラルネットワークで行うことによって、保存性を担保した機械学習モデル FluxGNN が構築できます。実際、このようにして構成した FluxGNN は (局所的な) 保存性を持つ機械学習モデルであり、逆に (局所的な) 保存性を持つ機械学習モデルは FluxGNN のみであるということが数学的に証明できます。つまり、保存性を実現したければ FluxGNN を使う以外にないということがわかるわけです。
ここで、GNN とはグラフニューラルネットワーク (Graph Neural Network) の略であり、GNN はメッシュや点群など、物理シミュレーションで典型的に使用されるデータ構造の学習・予測に適している機械学習モデルであることが知られています。下図のように、FVM での数値流束が GNN における相互作用を記述するニューラルネットワークである message 関数に対応していることがわかるため、FluxGNN は文字通り GNN の一種でもあるとみなせます。
また、対称性に関してはすでに多くの関連研究があるため詳細は割愛しますが、大まかな考え方のみ示します。物理シミュレーションにおいて形状の表現に使用されるメッシュの空間刻み幅や時間の離散化に用いられる時間刻み幅を用いて物理量を無次元化し、その無次元量にのみニューラルネットワークを適用することによってスケール変換による外挿を防ぐことができます。これにより、拡大縮小に対する対称性が実現できます。回転など他の変換に対する対称性は、過去の記事 (IsoGCN: 物理シミュレーションのための機械学習モデル や 物理屋のための機械学習講義「対称性のある機械学習による物理現象の解析」) を参照してください。
- 厳密には隣り合うセル間のやりとりでの保存性なので、局所的な保存性が成り立っています。局所的な保存性があっても解析領域全体で大域的な保存性が成り立つとは限らず、例えば領域内で物理量の湧き出しがあったり境界からの流入があったりする場合は、物理量の大域的な保存性は成立しません。↑
数値実験
次に、FluxGNN の汎化性能の高さを実証するために、流体現象の物理シミュレーションを学習させた数値実験の結果を紹介します。対象となる現象は、密度差がある流体の混相流です。この密度差によって浮力が生じ、浮力によって流れが駆動されます。例として、煙が立ち上っていくような現象を想像していただければわかりやすいと思います。
精密な物理シミュレーションの結果を正解として、それらのデータを学習したさまざまな機械学習モデルの予測結果を下図に示します。結果は、以下の 4 つの条件において評価しました:
- Test: 通常の機械学習のテストデータセット同様、学習データと近い形状が学習データにはない形状における評価。
- Rotation: Test データに回転変換をほどこしたもの。Test と本質的にはまったく同じ現象。
- Scaling: Test データに拡大変換をほどこしたもの。Test と本質的にはまったく同じ現象。
- Taller: 学習データと大きく異なる形状における評価。
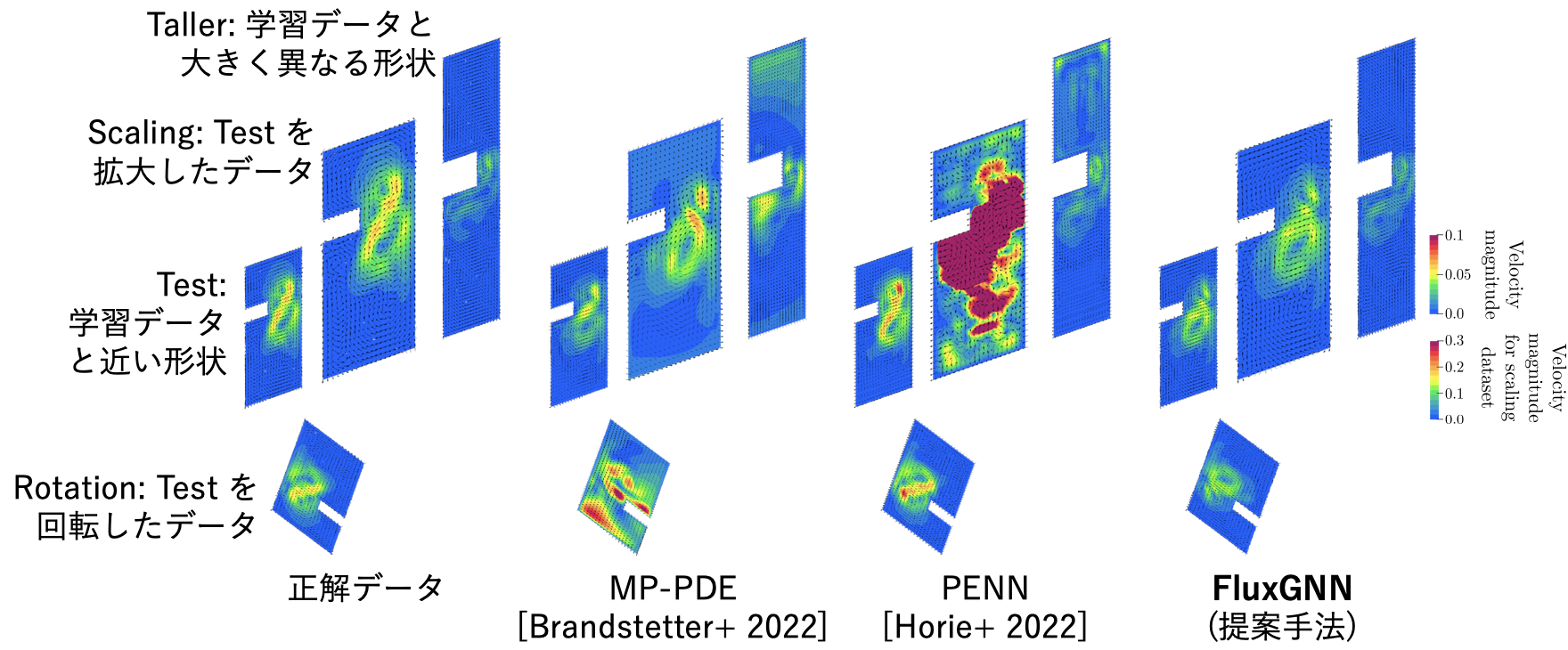
図からわかるとおり、FluxGNN では回転や拡大縮小に対する対称性があるため、他の手法と比較して精度の低下が見られません。なお、我々のグループの以前の研究である PENN では回転に対する対称性はあるため Rotation では精度が低下していませんが、Scaling では大きく精度が下がっています。さらに、FluxGNN が持つ保存性と対象性によって、学習データとは大きく異なる形状である Taller においても、精度の低下が見られませんでした。したがって、FluxGNN は未知の形状においても高い精度を持つという、ものづくりにおける性能評価のために都合のよい性質があることがわかります。
おわりに
本記事では、保存性や対称性を満たす機械学習モデルである FluxGNN について解説しました。また、FluxGNN ではこれらの物理現象の性質を満たすことから、学習データとは大幅に異なるデータに対しても高い精度で予測が行えることが実証されていることを見ました。今後は、FluxGNN をさまざまな対象に適用し、ものづくりのさらなる高度化のための研究開発を進めていきます。
また、弊社では FluxGNN に限らず最新の研究成果の知見を活かし、空力・熱流体・混相流などを含めた多様な流体現象の機械学習・最適化のソリューションを提供しております。もしご興味がありましたらぜひお問合せフォームからご連絡ください。







